.jpg)
Holiness David Running Eagle beats the sacred drum and says to Song of Heaven: flow
The beat of the drum is what I hear, a feeling of love from our Mother Deer, softness and a warm embrace, sets a steady base. Bum bum drum tum tum bum.
The beating of the drum, like one heart beat, that does lead all that lives , it gives a kiss, breath in breath out, in silence and out loud, the wave is flowing. It just keeps on going to and fro, here and there, at the heart where we do care.
Blessed are thee, who sets themselves free, to reach a hand and make a stand, rainbows come home and *glome (to unite upon the red road, the sacred directions we walk home, into the crystalline flow)!Twin Deer Mother (White Buffalo Calf Woman) Hums and Sings:
And when its time, we demand all heart be sublime, And when we shine, sacred hearts do make up our minds. Stars in heaven, shine down upon me. Like a door. Open up and be free. And where it's darkness shines, my heart will know it's blind. I must use my heart. I must be the saint God gifted me. I will walk through that door, even if it's all dark and closed to me.
I will fly across heaven to find true love. I will seek, the kite that flies in the sky and plays for keep. And it will be bright, like clouds in the night. It will be grand, because I am part of man.
Hold me close, to where I must go. Know the place, where heaven hands do flow. Gain a heart, and know how to make the sacred dart. Lean on love and bring heaven home to me and you,
whence we came. It was heaven's day, upon us. Where we flow, is heaven's dreams upon us.
And I know it's faint, but it's a dark place to begin. And you must learn to shine. To bring heaven's sublime. Let us dream. Fill our world with heaven's dance. Hold my hand, and we can take a chance.
Southern Season, our Song of Heaven: Thank youTwin Deer Mother: Thank you. Love and blessings to you. Blessings to the nine directions. Holiness David says have a wonderful day and thanks for talking with us. Thanks beloved. Sweet dreams, awake for you. Aho ah, brotherhood, sisterhood rules, whoo hooo. Love you.
Southern Season, our Song of Heaven: Love and Blessings 9 directions back. Sweet dreams and fly high! Aho! Love you too!
Hoop one: We recognize you as a spiritual being and welcome you to one family consciousness. Here at Active-Indigos, we respectfully address the ascension, flesh or light and descending, soul or darkness, process while creating local sanctuaries on earth. Thinking globally and acting locally while networking all spiritual communities and educating the workplace.
Elders come to be, when they stand to be free, to be heard of justice door, the place where all live to be, united in heart. United when apart. United in Spirit, to hold and have Heaven, inside the beginning, the Elders of the World. Who come home to what is heard. Who use love beyond all words. To know when LOVE is true. And Knows when we need the views, of pure light, of pure dark, of heaven and earth, abound as One who's gonna win. It's the Elders who refuse to budge and look for hues, instead sea with their hearts, and prays about all things in the heart.
I bless me. I bless the world. I bless you.
*Image, a glome: Stereographic projection of the hypersphere's parallels (red), meridians (blue) and hypermeridians (green). Due to conformal property of Stereographic projection, the curves intersect each other orthogonally (in the yellow points) as in 4D. All curves are circles: the curves that intersect (0,0,0,1); have infinite radius (= straight line).
*Glome definition:
A 3-sphere is also called a "glome" or a hypersphere, although the term hypersphere can in general describe any n-sphere for n ≥ 3. In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space. Just as an ordinary sphere (or 2-sphere) is a two dimensional surface that forms the boundary of a ball in three dimensions, a 3-sphere is an object with three dimensions that forms the boundary of a ball in four dimensions. A 3-sphere is an example of a 3-manifold. A 3-sphere can be constructed topologically by "gluing" together the boundaries of a pair of 3-balls (six sides, the sacred blessings or the crystalline stone). In three dimensions, there is always a hidden fourth side, or relative point, like the equation 0,0,0,1 (four sacred directions, three points of light and a point of darkness, or gray, grandmother dream space).
All curves are circles: the curves that intersect (0,0,0,1); have infinite radius (= straight line). We therefore continue to travel round and round, four sacred directions upon a path, around in a circle, to where it ends and where it begins. This is evolution. This is the river in life, that we all stream towards, relative to and journey on an evolutionary scale. The laws of physics and science are the understandings of God's principles. It is Song of Heaven that reminds us, of this sacred path, we all adhere to, the glome.
*Glome definition continues:
Strategies for polytopes
* Start with lower-dimensional analogs (in the tradition of Flatland)
* Projecting into a lower-dimensional space
* Unfolding
* Cross-sections over time as higher-dimensional figure passes through lower-dimensional space
For 4D objects, begin with the tesseract (or 4D hypercube, the 4D analog of a cube) and the pentachoron (or 4-simplex, the 4D analog of a tetrahedron). (four sacred directions)
Strategies for curved figures
Again, begin with the simplest figure: a 4D hypersphere (a.k.a. glome). Somewhat unintuitively to non-mathematicians, this is also termed a 3-sphere, because any point on its "surface" can be specified with three coordinates. (The familiar 3D sphere, such as a globe of the Earth, is called a 2-sphere for analogous reasons; you can specify any point on its surface with only lines of latitude and longitude.)
* Slicing (gluing successive cross-sections together)
* Suspension (connect every point on a 3D sphere to two points in higher space, like a hammock; this yields a topological glome, though not a geometric one.
* "Cone" gluing (similar to the above; take two 3D spheres and connect each one to a point in 4-space (a different point for each). Paste the two spheres together, point-for-point, around their surfaces.)
* Hopf fibration
In coordinates, a 3-sphere with center (C0, C1, C2, C3) and radius r is the set of all points (x0, x1, x2, x3) in real, 4-dimensional space (R4) such that \sum_{i=0}^3(x_i - C_i)^2 = ( x_0 - C_0 )^2 + ( x_1 - C_1 )^2 + ( x_2 - C_2 )^2+ ( x_3 - C_3 )^2 = r^2. The 3-sphere centered at the origin with radius 1 is called the unit 3-sphere and is usually denoted S3: S^3 = \left\{(x_0,x_1,x_2,x_3)\in\mathbb{R}^4 : x_0^2 + x_1^2 + x_2^2 + x_3^2 = 1\right\}. It is often convenient to regard R4 as the space with 2 complex dimensions (C2) or the quaternions (H). The unit 3-sphere is then given by S^3 = \left\{(z_1,z_2)\in\mathbb{C}^2 : |z_1|^2 + |z_2|^2 = 1\right\} or S^3 = \left\{q\in\mathbb{H} : |q| = 1\right\}.
The last description is often the most useful. It describes the 3-sphere as the set of all unit quaternions—quaternions with absolute value equal to unity. Just as the unit circle is important for planar polar coordinates, so the 3-sphere is important in the polar view of 4-space involved in quaternion multiplication. See polar decomposition of a quaternion for details of this development of the three-sphere.
Elementary properties
The 3-dimensional volume (or hyperarea) of a 3-sphere of radius r is 2\pi^2 r^3 \, while the 4-dimensional hypervolume (the volume of the 4-dimensional region bounded by the 3-sphere) is \begin{matrix} \frac{1}{2} \end{matrix} \pi^2 r^4.
Every non-empty intersection of a 3-sphere with a three-dimensional hyperplane is a 2-sphere (unless the hyperplane is tangent to the 3-sphere, in which case the intersection is a single point). As a 3-sphere moves through a given three-dimensional hyperplane, the intersection starts out as a point, then becomes a growing 2-sphere which reaches its maximal size when the hyperplane cuts right through the "equator" of the 3-sphere. Then the 2-sphere shrinks again down to a single point as the 3-sphere leaves the hyperplane.
Topological properties
A 3-sphere is a compact, connected, 3-dimensional manifold without boundary. It is also simply-connected. What this means, loosely speaking, is that any loop, or circular path, on the 3-sphere can be continuously shrunk to a point without leaving the 3-sphere. The Poincaré conjecture proposes that the 3-sphere is the only three dimensional manifold with these properties (up to homeomorphism). This conjecture was proved correct in 2003 by Grigori Perelman.
The 3-sphere is homeomorphic to the one-point compactification of \mathbb{R}^3. Generally, any topological space which is homeomorphic to the 3-sphere is called a topological 3-sphere.
The homology groups of the 3-sphere are as follows: H0(S3,Z) and H3(S3,Z) are both infinite cyclic, while Hi(S3,Z) = {0} for all other indices i. Any topological space with these homology groups is known as a homology 3-sphere. Initially Poincaré conjectured that all homology 3-spheres are homeomorphic to S3, but then he himself constructed a non-homeomorphic one, now known as the Poincaré homology sphere. Infinitely many homology spheres are now known to exist. For example, a Dehn filling with slope 1/n on any knot in the three-sphere gives a homology sphere; typically these are not homeomorphic to the three-sphere.
As to the homotopy groups, we have π1(S3) = π2(S3) = {0} and π3(S3) is infinite cyclic. The higher homotopy groups (k ≥ 4) are all finite abelian but otherwise follow no discernible pattern. For more discussion see homotopy groups of spheres. Homotopy groups of S3
The 3-sphere is naturally a smooth manifold, in fact, a closed embedded submanifold of R4. The Euclidean metric on R4 induces a metric on the 3-sphere giving it the structure of a Riemannian manifold. As with all spheres, the 3-sphere has constant positive sectional curvature equal to 1/r2 where r is the radius.
Much of the interesting geometry of the 3-sphere stems from the fact that the 3-sphere has a natural Lie group structure given by quaternion multiplication (see the section below on group structure). The only other spheres with such a structure are the 0-sphere and the 1-sphere (see circle group).
Unlike the 2-sphere, the 3-sphere admits nonvanishing vector fields (sections of its tangent bundle). One can even find three linearly-independent and nonvanishing vector fields. These may be taken to be any left-invariant vector fields forming a basis for the Lie algebra of the 3-sphere. This implies that the 3-sphere is parallelizable. It follows that the tangent bundle of the 3-sphere is trivial. For a general discussion of the number of linear independent vector fields on a n-sphere see the article vector fields on spheres.
There is an interesting action of the circle group T on S3 giving the 3-sphere the structure of a principal circle bundle known as the Hopf bundle. If one thinks of S3 as a subset of C2, the action is given by (z_1,z_2)\cdot\lambda = (z_1\lambda,z_2\lambda)\quad \forall\lambda\in\mathbb T.
The orbit space of this action is homeomorphic to the two-sphere S2. Since S3 is not homeomorphic to S2×S1, the Hopf bundle is nontrivial.
Topological construction
Two convenient constructions for the topologist are the reverse of "slicing in half" and "puncturing".
A 3-sphere can be constructed topologically by "gluing" together the boundaries of a pair of 3-balls. The boundary of a 3-ball is a 2-sphere, and these two 2-spheres are to be identified. That is, imagine a pair of 3-balls of the same size, then superpose them so that their 2-spherical boundaries match, and let matching pairs of points on the pair of 2-spheres be identically equivalent to each other.
The interiors of the 3-balls do not match: only their boundaries. In fact, the fourth dimension can be thought of as a continuous scalar field, a function of the 3-dimensional coordinates of the 3-ball, similar to "temperature". Let this "temperature" be zero at the 2-spherical boundary, but let one of the 3-balls be "hot" (have positive values of its scalar field) and let the other 3-ball be "cold" (have negative values of its scalar field). The "hot" 3-ball could be thought of as the "hot hemi-3-sphere" and the "cold" 3-ball could be thought of as the "cold hemi-3-sphere". The temperature is highest at the hot 3-ball's very center and lowest at the cold 3-ball's center.
This construction is analogous to a construction of a 2-sphere, performed by joining the boundaries of a pair of disks. A disk is a 2-ball, and the boundary of a disk is a circle (a 1-sphere). Let a pair of disks be of the same diameter; superpose them so that their circular boundaries match, then let corresponding points on the circular boundaries become equivalent identically to each other. The boundaries are now glued together. Now "inflate" the disks. One disk inflates upwards and becomes the Northern hemisphere and the other inflates downwards and becomes the Southern hemisphere.
It is possible for a point traveling on the 3-sphere to move from one hemi-3-sphere to the other hemi-3-sphere by crossing the 2-spherical boundary, which could be thought of as a "3-quator" — analogous to an equator on a 2-sphere. The point would seem to be bouncing off the 3-quator and reversing direction of motion in 3-D, but also its "temperature" would become reversed, e.g. from positive on the "hot hemi-3-sphere" to zero on the 3-quator to negative on the "cold hemi-3-sphere".
Unpuncturing
Consider a topological 2-sphere to be a seamless balloon. When punctured and flattened, the missing point becomes a circle (a 1-sphere) and the remaining balloon surface becomes a disk (a 2-ball) inside the circle. In the same way, a 3-ball is a punctured and flattened 3-sphere. To recreate the 3-sphere, merge all points on the 3-ball boundary (a 2-sphere) into a single point.
Another view of puncturing is stereographic projection. Rest the South Pole of a 2-sphere on an infinite plane, and draw lines from the North Pole through the sphere to intersect the plane. Each sphere point corresponds to a unique plane point, and vice versa, excepting the North Pole itself. The balloon has been stretched to infinity. Stereographic projection of a 3-sphere (except for the projection point) fills all of 3-space in the same manner. A benefit of this correspondence is that geometric spheres in 3-space map to geometric spheres of the 3-sphere, and planes in 3-space map to spheres containing the Pole.
Another view is a "shooting map". Place a marble at the South Pole and give it a flick of a measured strength in a chosen direction. Assuming the marble stays on the sphere and rolls without friction, its position after a fixed time interval (say, 1 second) will be some definite point of the sphere. Plotting direction in the plane and strength as radius, the North Pole is equally far away in every direction; this is the equivalent of the punctured balloon. Performing the same shooting experiment on the 3-sphere gives a map on the 3-ball. When the 3-sphere is considered a Lie group, the marble paths are one-parameter subgroups, the 3-ball is the tangent space at the identity (taken to be the South Pole), and the mapping to the 3-sphere is the exponential map.
The justification for creating general relativity came from the equivalence principle, which dictates that free-falling observers are the ones in inertial motion. Roughly speaking, the principle states that the most obvious effect of gravity – things falling down – can be eliminated by making the transition to a reference frame that is in free fall, and that in such a reference frame, the laws of physics will be approximately the same as in special relativity. A consequence of this insight is that inertial observers can accelerate with respect to each other. For example, a person in free fall in an elevator whose cable has been cut will experience weightlessness: objects will either float alongside him or her, or drift at constant speed. In this way, the experiences of an observer in free fall will be very similar to those of an observer in deep space, far away from any source of gravity, and in fact to those of the privileged ("inertial") observers in Einstein's theory of special relativity. Einstein realized that the close connection between weightlessness and special relativity represented a fundamental property of gravity.
Einstein's key insight was that there is no fundamental difference between the constant pull of gravity we know from everyday experience and the fictitious forces felt by an accelerating observer (in the language of physics: an observer in a non-inertial reference frame). So what people standing on the surface of the Earth perceive as the 'force of gravity' is a result of their undergoing a continuous physical acceleration which could just as easily be imitated by placing an observer within a rocket accelerating at the same rate as gravity (9.81 m/s²).
This redefinition is incompatible with Newton's first law of motion, and cannot be accounted for in the Euclidean geometry of special relativity. To quote Einstein himself: “If all accelerated systems are equivalent, then Euclidean geometry cannot hold in all of them.” Thus the equivalence principle led Einstein to develop a gravitational theory which involves curved space-times. Paraphrasing John Wheeler, Einstein's geometric theory of gravity can be summarized thus: spacetime tells matter how to move; matter tells spacetime how to curve.
Theoretical justification
General relativity is based upon a set of fundamental principles and assumptions which guided its development.General principle of relativity
The laws of physics must be the same for all observers (accelerated or not).Principle of general covariance
The laws of physics must take the same form in all coordinate systems. In addition, the principle of general covariance forces that mathematics to be expressed using tensor calculus. Tensor calculus permits a manifold as mapped with a coordinate system to be equipped with a metric tensor of spacetime which describes the incremental (spacetime) intervals between coordinates from which both the geodesic equations of motion and the curvature tensor of the spacetime can be ascertained.Inertial and geodesic motion
Converging geodesics: two lines of longitude (green) that start out in parallel at the equator (red) but converge to meet at the pole
Geometry of spacetime
On a curved two-dimensional surface, it is still possible to define lines that are as straight as possible, so called geodesics – for instance, on the spherical surface of the Earth, the lines of longitude, the equator, and other great circles. But the properties of these lines will differ from those of straight lines. Analogously, the world lines of test particles in free fall are spacetime geodesics – they are the straightest possible lines in spacetime, but there will be important differences between them and the truly straight lines in the gravity-free spacetime of special relativity: in special relativity, parallel geodesics remain parallel; in a gravitational field with tidal effects, such as the case of two bodies falling side by side towards the center of the Earth, initially parallel geodesics converge as the bodies move towards each other.Local Lorentz invariance
The laws of special relativity apply locally for all inertial observers.Einstein field equations
In 1907, Hermann Minkowski introduced a geometry that included not only the three (apparent) dimensions of space, but also a fourth dimension of time in order to present a geometric formulation of Einstein's special theory of relativity. Building upon the mathematical work of Carl Friedrich Gauss and Bernhard Riemann, Einstein postulated that Minkowski's spacetime could be treated as a 4-dimensional manifold which is curved by the presence of mass, energy and momentum (which, taken together, is known as stress-energy). Because Einstein previously determined that mass and energy are equivalent (E = mc²), gravitation is not caused by mass alone (as predicted by Newtonian physics) but by the distortion of spacetime by a combination of mass, energy, and momentum. The Einstein field equations describe the relationship between stress-energy and the curvature of spacetime.The curvature of spacetime (caused by the presence of stress-energy of massive entities like the Sun or Earth) can be analogized by placing a heavy object such as a bowling ball on a trampoline will produce a 'dent' in the trampoline. The larger the mass, the bigger the amount of curvature. A relatively light object placed in the vicinity of the 'dent', such as a ping-pong ball, will accelerate towards the bowling ball in a manner governed by the 'dent'. Firing the ping-pong ball at some suitable combination of direction and speed towards the 'dent' will result in the ping-pong ball 'orbiting' the bowling ball. This is analogous to the Moon orbiting the Earth, for example. Similarly, in general relativity massive objects do not directly impart a force on other massive objects as hypothesized in Newton's action at a distance idea. Instead (in a manner analogous to the ping-pong ball's response to the bowling ball's dent rather than the bowling ball itself), other massive objects respond to how the first massive object curves spacetime.
The mathematics of general relativity
Coordinates with the same difference in longitude at different latitudes are different absolute distances. Someone at the equator, moving 30 degrees of longitude westward (magenta line) corresponds to a distance of roughly 3,300 kilometers (2,051 mi); for someone at a latitude of 55 degrees, moving 30 degrees of longitude westward (blue line) covers a distance of merely 1,900 kilometers (1,181 mi)
Using a combination of calculus and metrics called metric tensors, the Einstein field equations (EFE) describe how stress-energy causes curvature of spacetime and are usually written in abstract index notation (a mathematical shorthand) as:
Solutions of EFEs
Any spacetime with an associated distribution of matter for which the curvature of spacetime and the energy and momentum of matter do satisfy these conditions is called a solution of Einstein's equations. These solutions are metrics of spacetime which describe the structure of spacetime given the stress-energy and coordinate mapping used to obtain that solution. For any model universe in which matter and geometry are meant to obey the laws of general relativity, Einstein's equations define ten independent conditions that must be fulfilled simultaneously at each point in spacetime. Being non-linear differential equations, the EFE often defy exact solutions; however, many such solutions are known. The simplest solution is Minkowski spacetime, the spacetime of special relativity. Other important solutions describe the gravitational field around a spherically symmetric massive object (Schwarzschild solution, 1916) or gravity and geometry in an expanding universe (Friedmann-Lemaître-Robertson-Walker solution).The EFE are the identifying feature of general relativity. Other theories built out of the same premises include additional rules and/or constraints. The result almost invariably is a theory with different field equations (such as Brans-Dicke theory, teleparallelism, Rosen's bimetric theory, and Einstein-Cartan theory)
Modification of other theories
Because general relativity enabled a paradigm shift away from Newtonian mechanics which had underpinned the physical sciences to that time, previous theories of inertia, gravitation, electromagnetism, and quantum mechanics had to adopt new geometrical framework and assumptions. While some of these have been validated, there is still a theoretical gap between the assumptions in quantum mechanics and general relativity.Predictions of general relativity
Gravitational effects
Gravitational redshifting
The gravitational redshift of a light wave escaping from the surface of a massive body
Assume that there are two observers, both of them at rest relative to a massive body. When the observer closer to the massive object sends some light to a second observer that is at rest higher up, the light will be red-shifted; the second observer will measure a lower frequency for the light than the first. Conversely, light sent from the second observer to the first will be blue-shifted (shifted towards higher frequencies). This is caused by an observer at a higher gravitational potential being accelerated (with respect to the local inertial frames of reference) away from the source of a beam of light as that light is moving towards that observer. Gravitational redshifting has been confirmed by the Pound-Rebka experiment.
Gravitational time dilation
A related effect is gravitational time dilation, under which clocks will run slower at lower gravitational potentials (deeper within a gravity well). For the same light wave, the second observer measures a lower frequency than the first; evidently, the second observer's clocks are running faster than those of the first observer. The same effect can also be derived in other ways (notably by transporting clocks back and forth and reconstructing the effect of location on their tick rate). Generally, clocks that are further down in a gravitational field tick more slowly than those that are higher up. This effect has been directly confirmed by the Hafele-Keating experiment and GPS.Gravitational time dilation has as a consequence another effect called the Shapiro effect (also known as gravitational time delay). Shapiro delay occurs when signals take longer to move through a gravitational field than they would in the absence of the gravitational field. This effect was discovered through the observations of signals from spacecraft and pulsars passing behind the Sun as seen from the Earth.
Gravitational lensing
Einstein cross: four images of the same astronomical object, produced by a gravitational lens
In a similar way, Einstein also derived another effect, the gravitational deflection of light where light rays are bent downward in a gravitational field. An important example of this is starlight being deflected as it passes the Sun; in consequence, the positions of stars observed in the Sun's vicinity during a solar eclipse appear shifted by up to 1.75 arc seconds. This effect was first measured by a British expedition directed by Arthur Eddington. Subsequent observations of the deflection of the light of distant quasars by the Sun, which utilize highly accurate techniques of radio astronomy, have confirmed Eddington's results with significantly higher accuracy.
A special type of gravitational lensing occurs in Einstein rings and arcs. The Einstein ring is created when an object is directly behind another object with a uniform gravitational field. In that case, the light from the more distant object becomes a ring around the closer object. If the more distant object is slightly offset to one side and/or the gravitational field is not uniform, partial rings (called arcs) will appear instead.
Finally, in our own galaxy a star can appear to be brightened when compact massive foreground object is sufficiently aligned with it. In that case, the magnified and distorted images of the background star due to the gravitational bending of light cannot be resolved. This effect is called microlensing, and such events are now regularly observed.
Gravitational lensing has developed into a tool of observational astronomy, where it is used (among other things) to determine the masses of certain objects, detect the presence of dark matter, and provide an independent estimate of the Hubble constant.
Orbital effects
Newtonian (red) vs. Einsteinian orbit (blue) of a lone planet orbiting a star
A related effect is geodetic precession. This is a precession of the poles of a spinning object due to the effects of parallel transport in a curved space-time. This effect is not expected in Newtonian gravity. The prediction of geodetic precession was tested and verified by the Gravity Probe B experiment to a precision of better than 1 percent.
Another effect is that of orbital decay due to the emission of gravitational radiation by a co-rotating system. It is observable in closely orbiting stars as an ongoing decrease in their orbital period. This effect has been observed in binary pulsar systems.
Frame dragging
Frame dragging is where a rotating massive object "drags" space-time along with its rotation. In essence, an observer who is distant from a rotating massive object and at rest with respect to its center of mass will find that the fastest clocks at a given distance from the object are not those which are at rest (as is the case for a non-rotating massive object). Instead, the fastest clocks will be found to have component of motion around the rotating object in the direction of the rotation. Similarly, it will be found by the distant observer that light moves faster in the direction of the rotation of the object than against it. Frame dragging will also cause the orientation of a gyroscope to change over time. For a spacecraft in a polar orbit, the direction of this effect is perpendicular to the geodetic precession mentioned above. Gravity Probe B is using this feature to test both frame dragging and the geodetic precession predictions.Black holes
 |
| An illustration of a rotating black hole at the center of a galaxy |
The disappearance of light and matter within a black hole may be thought of as their entering a region where all possible world lines point inwards. Stephen Hawking has predicted that black holes can "leak" mass, a phenomenon called Hawking radiation, a quantum effect not in violation of general relativity. Certain types of black holes are thought to be the final state in the evolution of massive stars. Supermassive black holes are thought to be present in the cores of most galaxies, and are thought to play a key role in galactic evolution. Numerous black hole candidates are known. These include the supermassive object associated with Sagittarius A* at the center of our galaxy
Matter falling onto a compact object is one of the most efficient mechanisms for releasing energy in the form of radiation, and matter falling onto black holes is thought to be responsible for some of the brightest astronomical phenomena imaginable, such as quasars and other types of active galactic nuclei.
Cosmology
Although it was created as a theory of gravitation, it was soon realized that general relativity could be used to model the universe, and so gave birth to the field of physical cosmology. The central equations for physical cosmology are the Friedmann-Lemaître-Robertson-Walker metric, which are the cosmological solution of the Einstein field equations. This metric predicts that the universe must be dynamic: It must either be expanding, contracting, or switching between those states.At the time of the discovery of the Friedmann-Lemaître-Robertson-Walker metric, Einstein could not abide by the idea of a dynamic universe. In an attempt to make general relativity accommodate a static universe, Einstein introduced an alternative form of the field equations to accommodate a static universe solution in his theory:
However, the resultant static universe was unstable. Then in 1929 Edwin Hubble showed that the redshifting of light from distant galaxies indicates that they are receding from our own at a rate which is proportional to their distance from us. This demonstrated that the universe is indeed expanding. Hubble's discovery ended Einstein's objections and his use of the cosmological constant.
The equations for an expanding universe become singular when one goes far enough back in time, and this primordial singularity marks the formation of the universe. That event has come to be called the Big Bang. In 1948, Ralph Asher Alpher and George Gamov published an article describing this event and predicting the existence of the cosmic microwave background radiation left over from the Big Bang. In 1965, Arno Penzias and Robert Wilson first observed the background radiation, confirming the Big Bang theory.
| What is dark matter? Do the phenomena attributed to dark matter point not to some form of matter but actually to an extension of gravity? |  |
Recently, observations of distant supernovae have indicated that the expansion of the universe is currently accelerating. This was unexpected since Friedmann-Lemaître-Robertson-Walker metric calls for a universe that only contains visible matter to have a decelerating expansion. In the modern cosmological models, most energy in the universe is in forms that have never been detected directly, namely dark energy and dark matter. However, for a universe that is 4% baryonic matter, 26% dark matter, and 70% dark energy, the Friedmann-Lemaître-Robertson-Walker metric takes on a form that is consistent with observation. There is also an irony in that the dark energy can be modeled using Einstein's cosmological constant, but with a value that enhances the dynamic nature of the universe instead of muting it. There have been several (controversial) proposals to obviate the need for these enigmatic forms of matter and energy by modifying the laws governing gravity and the dynamics of cosmic expansion (for example, modified Newtonian dynamics).
Other predictions
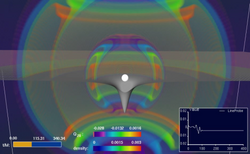
Simulation based on the equations of general relativity: a star collapsing to form a black hole while emitting gravitational waves
The theory also predicts exotic forms of Gravitational radiation. As gravity is substantially weaker than other physics forces, currently only extremely violent interactions (like merging neutron stars and/or black holes) are expected to emitting observable radiation. A number of land-based gravitational wave detectors are in operation, with the aim of detecting gravitational waves directly. Orbital decay, as described above, may be likened to gravitational radiation as well. Graviational radiation may also be observed in subatomic particles called gravitons or quadrupole and higher order multipole moments, but these have been experimentally observed or verified.
Validity
Because general relativity has passed every unambiguous observational and experimental test to which it has been subjected so far, it is almost universally accepted by the scientific community. However, while it is a highly successful model of gravitation and cosmology, there are substantial theoretical inconsistencies between general relativity, quantum mechanics, and the spacetime singularities associated with black holes.Quantum mechanics
| How can the theory of quantum mechanics be merged with the theory of general relativity to produce a so-called "theory of everything"? | |
Notably, in contrast to all other modern theories of fundamental interactions, general relativity is a classical theory which does not include the effects of quantum physics. The question of what general relativity looks like at a quantum level is often called a theory of quantum gravity or Theory of everything. This subject remains one of the great open questions of physics. While there are promising candidates such as string theory and loop quantum gravity, there is at present no consistent and complete theory of quantum gravity which reconciles Einstein's geometric picture of gravity with the laws of the quantum world.
Spacetime signularities
It is a longstanding hope that the theory of quantum gravity would also do away with spacetime singularities. Such singularities are boundaries ("ragged edges") of spacetime at which geometry becomes ill-defined; the best-known examples are the singularities inside black holes and at the Big Bang singularity at the beginning of the universe. If the laws of general relativity were to hold without any quantum modifications, then, by what are known as the singularity theorems, such singularities would indeed exist in our universe.For further reading, please visit http://encyclopedia.thefreedictionary.com/glome and about relativity http://en.wikipedia.org/wiki/User:Madcoverboy/Sandbox/General_relativity
Happier Cows, Thanks to Math
Here's a kind of offbeat one for you today. Scientists have come up with a mathematical model to explain (or attempt to explain) a pretty interesting aspect of bovine behavior.
If you've ever spent any time in a cow pasture, you learn two things pretty quickly. First, always watch where you walk. Second, cows tend to sit or stand in groups. If one of them is laying down, chances are, most of them are laying down. And, if one of them is walking around, chances are most of them are walking around.
So, um ... why is that, exactly? (The groupthink behavior, that is. I imagine you can figure out the watching-where-you-walk part on your own.)
Jie Sun and his friends over at Clarkson University think they've got an answer for you. It has to do with oscillators, looking at cows as a binary system. The result is, as the abstract puts it, "a mathematical model for daily activities of a cow (eating, lying down, and standing) in terms of a piecewise affine dynamical system."
In plain English, that means, cows tend to operate in synchronicity, just like we said earlier. We already knew that, so who needs math anyway?
Well, here's the takeaway. The more synchronicity, the happier the cows appear to be, according to Technology Review. And, along with that, you've got to talk about coupling — the proximity of a cow to his nearest neighbor. More coupling, according to the study, appears to create less synchronicity.
As a practical matter, the closer cows are jammed together, the less synchronized they are, and that's an indication that they're uncomfortable or unhappy. Think about how you feel on a crowded elevator.
The real-world upshot is this: Happy cows yield more (and better tasting) milk, cheese, or meat if that's your thing. If you cram a bunch of cattle into your standard factory farm conditions, you end up with yuckier product.
So, the ethical arguments against factory farming are clear. And, the public health arguments against factory farming are also pretty well-established. Now, add the mathematical argument. Factory farming just doesn't add up.
If you've ever spent any time in a cow pasture, you learn two things pretty quickly. First, always watch where you walk. Second, cows tend to sit or stand in groups. If one of them is laying down, chances are, most of them are laying down. And, if one of them is walking around, chances are most of them are walking around.
So, um ... why is that, exactly? (The groupthink behavior, that is. I imagine you can figure out the watching-where-you-walk part on your own.)
Jie Sun and his friends over at Clarkson University think they've got an answer for you. It has to do with oscillators, looking at cows as a binary system. The result is, as the abstract puts it, "a mathematical model for daily activities of a cow (eating, lying down, and standing) in terms of a piecewise affine dynamical system."
In plain English, that means, cows tend to operate in synchronicity, just like we said earlier. We already knew that, so who needs math anyway?
Well, here's the takeaway. The more synchronicity, the happier the cows appear to be, according to Technology Review. And, along with that, you've got to talk about coupling — the proximity of a cow to his nearest neighbor. More coupling, according to the study, appears to create less synchronicity.
As a practical matter, the closer cows are jammed together, the less synchronized they are, and that's an indication that they're uncomfortable or unhappy. Think about how you feel on a crowded elevator.
The real-world upshot is this: Happy cows yield more (and better tasting) milk, cheese, or meat if that's your thing. If you cram a bunch of cattle into your standard factory farm conditions, you end up with yuckier product.
So, the ethical arguments against factory farming are clear. And, the public health arguments against factory farming are also pretty well-established. Now, add the mathematical argument. Factory farming just doesn't add up.
Martin Matheny is a political consultant and animal welfare writer based in Athens, GA. Photo credit: John-Morgan. Thank you http://animals.change.org/blog/view/happier_cows_thanks_to_math
Bertram Kostant, Experimental evidence for the occurrence of E 8 in nature and the radii of the Gossett circles, Tuesday February 23, 3:00 at APM 6402, Department of Mathematics, U.C. San Diego.Abstract:
A recent experimental discovery involving the spin structure of electrons in a cold one dimensional magnet points to a model involving the exceptional Lie group E 8. The model predicts 8 particles the ratio of whose masses are the same as the ratios of the radii of the circles in the famous Gossett
diagram (going back to 1900) of what is now understood to be a 2 dimensional projection of the 240 roots of E 8 arranged in 8 concentric circles. The ratio of the radii of the two smallest circles (read 2 smallest masses) is the golden number. This beautifully has been found experimentally. The ratio of the radii of the other masses has been written down conjecturally by Zamolodchikov. This again agrees with the analogous statement for the radii of the Gossett circles.
Some time ago we found an operator A (very easily defined and reexpressed by Vogan as an element of the group algebra of the Weyl group) on 8-space whose spectrum is exactly the squares of the radii of the Gossett circles.
The operator A is written in terms of the coefficients n i of the highest root. In McKay theory the n i are the dimensions of the irreducible representations of the binary icosahedral group. Our result works for any simple Lie group not just E 8.
Posted by: John Baez on February 17, 2010
Thank you http://golem.ph.utexas.edu/category/2010/01/this_weeks_finds_in_mathematic_50.html
Pray With Elders around the World
